Logo

Menu

江苏专转本-线性代数-PreView

LiFasT
LiFasT
Published on 2024-12-23 / 101 Visits
0
1

前言

照例写点废话，这都已经成为传统了（笑）。本来想用Obsidian做笔记的，但是想了一下还要借助OneDrive才能多端共享，加上我自己不是很适应Obsidian的使用，比较麻烦，所以还是在网站上写吧。

这里的笔记的目的就是为我自己服务，所以写的比较主观，当然如果可以帮到任何人，我都很高兴。如果你发现这个上面有问题，你可以直接找我（既然你能看到这个，你肯定有办法找我），或者在下面留言，我非常喜欢开源共享，互帮互助。

这里我对内容结构的划分完全根据我自己学习的时候的感觉来的，部分内容可能反直觉或者不合理，还请见谅。其次这个并不是严格意义上的教材，所以我不会把一些抽象的概念放上来，我基本会用大白话来解释内容。

再提一点字吧：这是我的起点，是我的第一步。往后想想，以后还会遇到考研，乃至计算机图形学和引擎开发。若干年后，再回顾这个页面，也希望能感受到彼时彼刻的热情和动力，也能感受到年轻的我的执着。愿我的梦想成功，也祝愿看到这个文章的你心想事成。

行列式

在一切开始之前，有个大前提，即行列式它是一个值，且它的行列数相等。

行列式计算方法

根据定义计算（暴力算法）

仅推荐三阶以以下用这个方法，方法如下：

\begin{align*} \begin{vmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{vmatrix}&=a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}-a_{13}a_{22}a_{31}-a_{12}a_{21}a_{33}-a_{11}a_{23}a_{32} \end{align*}

根据性质转换（变为上下三角后定义算）

通过行列式的性质把一般的行列式转换为上下三角形的行列式，再通过定义计算，即只需要计算对角线乘积

根据展开定理计算（分块法）

定义：行列式等于它的任意一行（列）的各元素与其对应的代数余子式乘积之和

这种方法适用于存在0较多的一行（列），便于计算

按行展开

D=\begin{vmatrix}a_{11}&a_{12}&\cdots&a_{1n}\\a_{21}&a_{22}&\cdots&a_{2n}\\\vdots&\vdots&\ddots&\vdots\\a_{n1}&a_{n2}&\cdots&a_{nn}\end{vmatrix} D = \sum_{j = 1}^{n}a_{ij}A_{ij}， A_{ij}=(-1)^{i + j}M_{ij}

按列展开

D=\begin{vmatrix}a_{11}&a_{12}&\cdots&a_{1n}\\a_{21}&a_{22}&\cdots&a_{2n}\\\vdots&\vdots&\ddots&\vdots\\a_{n1}&a_{n2}&\cdots&a_{nn}\end{vmatrix} D=\sum_{i = 1}^{n}a_{ij}A_{ij}， A_{ij}=(-1)^{i + j}M_{ij}

行列式的种类

转置行列式

\vert A^T\vert=\vert A\vert
\begin{vmatrix}1&2&3\\4&5&6\\7&8&9\end{vmatrix} = \begin{vmatrix}1&4&7\\2&5&8\\3&6&9\end{vmatrix}

上三角、下三角行列式

上三角形行列式：\begin{vmatrix} a_{11} & a_{12} & a_{13} & \cdots & a_{1n} \\ 0 & a_{22} & a_{23} & \cdots & a_{2n} \\ 0 & 0 & a_{33} & \cdots & a_{3n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & a_{nn} \end{vmatrix}

下三角形行列式：\begin{vmatrix} a_{11} & 0 & 0 & \cdots & 0 \\ a_{21} & a_{22} & 0 & \cdots & 0 \\ a_{31} & a_{32} & a_{33} & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & a_{n3} & \cdots & a_{nn} \end{vmatrix}

计算该类型行列式的方法：主对角线元素的乘积

对角形行列式

\begin{vmatrix} a_{11} & 0 & 0 & \cdots & 0 \\ 0 & a_{22} & 0 & \cdots & 0 \\ 0 & 0 & a_{33} & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & a_{nn} \end{vmatrix}

行列式的性质

  • 性质一：经转置行列式的值不变

\begin{align*} \vert A^T\vert=\vert A\vert \end{align*}

  • 性质二：互换行列式的两行（列），行列式变号——即行列式前面加个负号

推论：如果行列式有两行（列）完全相同，则此行列式等于零

  • 性质三：若行列式某行（列）有公因子k，则可把公因子k提到行列式外面

注意：这里和矩阵并不一样，只能把某一行（列）的公因子k提出来，不能涉及到其他行（列）。若整体都有公因子，要全部提出来，要考虑到提出来几个，即要思考次方问题。如果要用某个数乘该行列式，也只能乘在一行（列）的元素上，并不能对所有元素进行乘法

推论：行列式中如果有两行（列）元素成比例，则此行列式等于零

  • 性质四：行列式的某一行（列）的各元素乘以同一个数然后加到另一行（列）对应的元素上去, 行列式的值不变

  • 性质五：若行列式的某一行（列）的元素都是两数之和，则此行列式等于两个行列式之和

D = \begin{vmatrix} a_{11}&\cdots&b_{1j}+c_{1j}&\cdots&a_{1n}\\ a_{21}&\cdots&b_{2j}+c_{2j}&\cdots&a_{2n}\\ \vdots&\ddots&\vdots&\ddots&\vdots\\ a_{n1}&\cdots&b_{nj}+c_{nj}&\cdots&a_{nn} \end{vmatrix} \text{ } D=\begin{vmatrix} a_{11}&\cdots&b_{1j}&\cdots&a_{1n}\\ a_{21}&\cdots&b_{2j}&\cdots&a_{2n}\\ \vdots&\ddots&\vdots&\ddots&\vdots\\ a_{n1}&\cdots&b_{nj}&\cdots&a_{nn} \end{vmatrix}+\begin{vmatrix} a_{11}&\cdots&c_{1j}&\cdots&a_{1n}\\ a_{21}&\cdots&c_{2j}&\cdots&a_{2n}\\ \vdots&\ddots&\vdots&\ddots&\vdots\\ a_{n1}&\cdots&c_{nj}&\cdots&a_{nn} \end{vmatrix}

注意：如果是在考虑行列式的加减法，首先确保是同阶，然后对应元素相加即可

余子式和代数余子式

余子式

定义：在n阶行列式中，把元素a_{ij}所在的第i行和第j列划去后，留下来的(n-1)阶行列式叫做元素a_{ij}的余子式，记作M_{ij}

例子：

在\begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{vmatrix}中，元素a_{21}的余子式M_{21}=\begin{vmatrix} a_{12} & a_{13} \\ a_{32} & a_{33} \end{vmatrix}

代数余子式

定义：A_{ij}=(-1)^{i + j}M_{ij}

例子：

在\begin{vmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{vmatrix}中，元素a_{23}的余子式M_{23}=\begin{vmatrix} 1 & 2 \\ 7 & 8 \end{vmatrix}，则代数余子式A_{23}=(-1)^{2 + 3}M_{23}=-\begin{vmatrix} 1 & 2 \\ 7 & 8 \end{vmatrix}

克拉默法则

先决条件：

方程组个数=未知数个数

系数行列式不能为0

使用方法（不仅适用于如下的二元，三元以上也可以）：

求解如下的二元线性方程组

\begin{cases} 3x - 2y = 12\\ 2x + y = 1 \end{cases}

首先求出系数行列式D=\begin{vmatrix}3& - 2\\2&1\end{vmatrix}=3\times1-(-2)\times2 = 7

用等式右边的常数替换第一列，得到D_x=\begin{vmatrix}12& - 2\\1&1\end{vmatrix}=12\times1-(-2)\times1 = 14

用等式右边的常数替换第二列，得到D_y=\begin{vmatrix}3&12\\2&1\end{vmatrix}=3\times1 - 12\times2 = - 21

根据克拉默法算出x和y的值

x=\frac{D_x}{D}=\frac{14}{7}=2\\ y=\frac{D_y}{D}=\frac{-21}{7}=-3

逆序数

逆序数绝对是最脑残的概念，所以放个AI，再放个做题方法

我这里简单说一下这个玩意\tau()

这玩意的算法：从左往后看，选一个数字，看它前面是否有比它大的，有就加，以此类推，写了个代码，应该是一个意思

int num = 0;
for(i=0;i<max;i++)
{
  for(j=i-1;j>=0;j--)
  {
    if(a[i] < a[j])  //判断是否比它大
      num++;
  }
}


范德蒙行列式

\begin{vmatrix} 1 & 1 & \cdots & 1 \\ x_1 & x_2 & \cdots & x_n \\ x_1^2 & x_2^2 & \cdots & x_n^2 \\ \vdots & \vdots & \ddots & \vdots \\ x_1^{n - 1} & x_2^{n - 1} & \cdots & x_n^{n - 1} \end{vmatrix} \prod_{1\leqslant j\lt i\leqslant n}(x_i - x_j)

可以把第一行的1，理解各个x的0次方

例如：\begin{vmatrix} 1 & 1 & 1 \\ x_1 & x_2 & x_3 \\ x_1^2 & x_2^2 & x_3^2 \end{vmatrix} =(x_2 - x_1)(x_3 - x_1)(x_3 - x_2)

即用后一个减前一个，从第二个开始，直到最后

矩阵

首先明确，行列式是一个值，而矩阵是个数表，且它的行列数可以不等

矩阵的运算

矩阵的加减法

条件：只有当两个矩阵是同型矩阵，即它们具有相同的行数和列数时，才能进行加减法运算

方法：对应元素相加减

矩阵的数乘

这里与行列式有区别，矩阵的数乘需要将每个元素都进行操作，而行列式只能操作一行或一列，具体看行列式的性质三

kA=\begin{pmatrix}ka_{11}&ka_{12}&ka_{13}\\ka_{21}&ka_{22}&ka_{23}\end{pmatrix}

数乘满足以下的规律：

k(lA)=(kl)A \qquad (k + l)A = kA + lA \qquad k(A + B)=kA + kB \qquad (kA)^T = kA^T

矩阵的乘法

条件：设矩阵A=(a_{ij})是m\times s矩阵，矩阵B=(b_{ij})是s\times n矩阵，即A的列数（一行的有几个玩意）等于B的行数（一列有几个玩意）时，A与B才能相乘，乘积记为AB，它是一个m \times n矩阵

注意：这里AB不能写成BA，不符合交换律，一般情况下这俩结果不一样

运算方法：定义太扯犊子了，就不放这里了，直接演示一下，如下

A=\begin{pmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{pmatrix} B=\begin{pmatrix}b_{11}&b_{12}\\b_{21}&b_{22}\end{pmatrix}
AB=\begin{pmatrix}a_{11}b_{11}+a_{12}b_{21}&a_{11}b_{12}+a_{12}b_{22}\\a_{21}b_{11}+a_{22}b_{21}&a_{21}b_{12}+a_{22}b_{22}\end{pmatrix}

我用大白话描述一下：前面的行元素乘以后面的列元素，然后加起来。也就是说第一个矩阵的第一行和第二个矩阵的第一列的各元素乘积之和就是乘完的矩阵的第一行第一列的元素，以此类推

矩阵乘法满足以下的规律：

(AB)C = A(BC) \qquad A(B + C)=AB + AC \qquad (B + C)A = BA + CA \\ k(AB)=(kA)B = A(kB) \qquad AB\neq BA

矩阵的类型

同型矩阵

就是行列数相等的矩阵

零矩阵

所有元素都是0的矩阵

方阵

行数和列数都等于n的矩阵，可以叫做n阶矩阵，或者叫做n阶方阵

由于矩阵乘法的条件，只有方阵才有幂的概念，所以一些性质和概念如下：

A^0=E \qquad A^1=A \qquad A^2=AA
A^aA^b=A^{a+b} \qquad (A^{a})^b=A^{ab}

一般情况下(AB)^c \ne A^cB^c，但当AB可以交换时，(AB)^c \ne A^cB^c

一般情况下(A+B)^2=A^2+AB+BA+B^2

单位矩阵和对角矩阵

单位矩阵就是主对角线元素都为1，其余为0，如下：

E_n=\begin{pmatrix} 1&0&\cdots&0\\ 0&1&\cdots&0\\ \vdots&\vdots&\ddots&\vdots\\ 0&0&\cdots&1 \end{pmatrix}

对于单位矩阵还有一个叫初等矩阵的概念，即单位矩阵经一次初等变换所得的矩阵称为初等矩（方）阵，更多内容在下面的初等变换小节里面

对角矩阵就是主对角线元素为任意值，其余为0，如下：

A=\begin{pmatrix} 2&0&0\\ 0& - 3&0\\ 0&0&5 \end{pmatrix}

阶梯型矩阵

这里可以细分成三种类型：行阶梯型矩阵、行最简形矩阵、标准型矩阵

任意矩阵 -> 行阶梯型矩阵 -> 行最简形矩阵 -> 标准型矩阵

任意矩阵通过有限次初等变换可以变为行阶梯型矩阵，再经过有限次初等变换可以变为行最简形矩阵，再经过有限次初等变换可以变为标准型矩阵

  • 行阶梯型矩阵

\begin{pmatrix} 1 & 2 & 3 & 4 \\ 0 & 5 & 6 & 7 \\ 0 & 0 & 0 & 8 \\ 0 & 0 & 0 & 0 \end{pmatrix}

以上就是行阶梯型矩阵，它的意思就是像阶梯一样，并且一次只能下一个格子，宽度不作限制，0行在最下面

  • 行最简形矩阵

\begin{pmatrix} 1 & 0 & 3 & 0 \\ 0 & 1 & 6 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \end{pmatrix}

定义：在行阶梯形矩阵的基础上，还满足：每个非零行的首非零元都为1，每个首非零元所在列的其余元素都为0

  • 标准型矩阵

\begin{pmatrix} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{pmatrix}

以上就是标准型矩阵，其要求就是左上角有个单位矩阵，其他元素为0

转置的矩阵

转置就是行列互换，即原来的第一行变成第一列，以此类推，例子如下：

A=\begin{pmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\end{pmatrix} A^T=\begin{pmatrix}a_{11}&a_{21}\\a_{12}&a_{22}\\a_{13}&a_{23}\end{pmatrix}

关于转置有如下的一些性质：

(A^T)^T = A \qquad (kA)^T = kA^T \qquad (A + B)^T = A^T + B^T \qquad (AB)^T = B^T A^T

矩阵的初等变换

三种初等变换

  • 交换两行（列）

  • 以非零数乘以某一行（列）

  • 把某一行（列）的若干倍加到另一行（列）

初等变换不会改变矩阵的秩，若矩阵A经过有限次初等变换变成矩阵B，则称A与B等价，记作A\sim B，这里两个矩阵秩相同

初等变换的用途：求逆矩阵、求线性方程组、求矩阵的秩

注意：这里不要和行列式搞混了，行列式的交换是要加负号的

初等矩阵

定义：对单位矩阵施行一次初等变换得到的矩阵称为初等矩阵

E_{ij}：交换i,j两行（列）得到的矩阵

E_i(k)：单位矩阵的第i行（列）乘以非零常数k得到的矩阵

E_{ij}(k)：单位矩阵的第j行乘k加到第i行（第i列乘k加到第j列）

行从后往前，列从前往后

矩阵的秩

k阶子式

首先明确，这是子式是一个行列式，这其实是一个语言的很难表达清楚的概念，让AI帮我个忙，如下：

对于一个m \times n的矩阵A，任取k行与k列（k \le min\{m,n\}），位于这些行列交叉处的k^2个元素，不改变它们在A中所处的位置次序而得到的k阶行列式，称为矩阵A的一个k阶子式。

以 4 阶矩阵为例：\begin{pmatrix}a_{11}&a_{12}&a_{13}&a_{14}\\a_{21}&a_{22}&a_{23}&a_{24}\\a_{31}&a_{32}&a_{33}&a_{34}\\a_{41}&a_{42}&a_{43}&a_{44}\end{pmatrix}

4 阶子式：本身就是一个 4 阶子式，即\begin{vmatrix}a_{11}&a_{12}&a_{13}&a_{14}\\a_{21}&a_{22}&a_{23}&a_{24}\\a_{31}&a_{32}&a_{33}&a_{34}\\a_{41}&a_{42}&a_{43}&a_{44}\end{vmatrix}

3 阶子式：例如取第 1、2、3 行和第 1、2、3 列，得到的 3 阶子式为\begin{vmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{vmatrix}

2 阶子式：例如取第 1、2 行和第 2、3 列，得到的 2 阶子式为\begin{vmatrix}a_{12}&a_{13}\\a_{22}&a_{23}\end{vmatrix}

1 阶子式：例如取第 3 行第 4 列的元素，得到的 1 阶子式为\begin{vmatrix}a_{34}\end{vmatrix}

矩阵的秩

定义：矩阵A中存在一个r阶子式不为0，且所有r+1阶子式（如果存在的话）全为0，则称数r为矩阵A的秩，记作r(A)。

秩的计算方法

  • 用秩的定义来算

  • 行列式（判断方阵是否满秩）

\vert A_n\vert \ne 0 \Leftrightarrow r(A_n) = n \\ \vert A_n\vert = 0 \Leftrightarrow r(A_n) < n

  • 初等行变换

根据初等变换，转化为阶梯型矩阵，非零行的个数就是矩阵的秩

注意：A=0 \Leftrightarrow r(A)=0

秩的重要结论

这里重点背一下，东西有点多，懒得写LaTex公式了，放个图

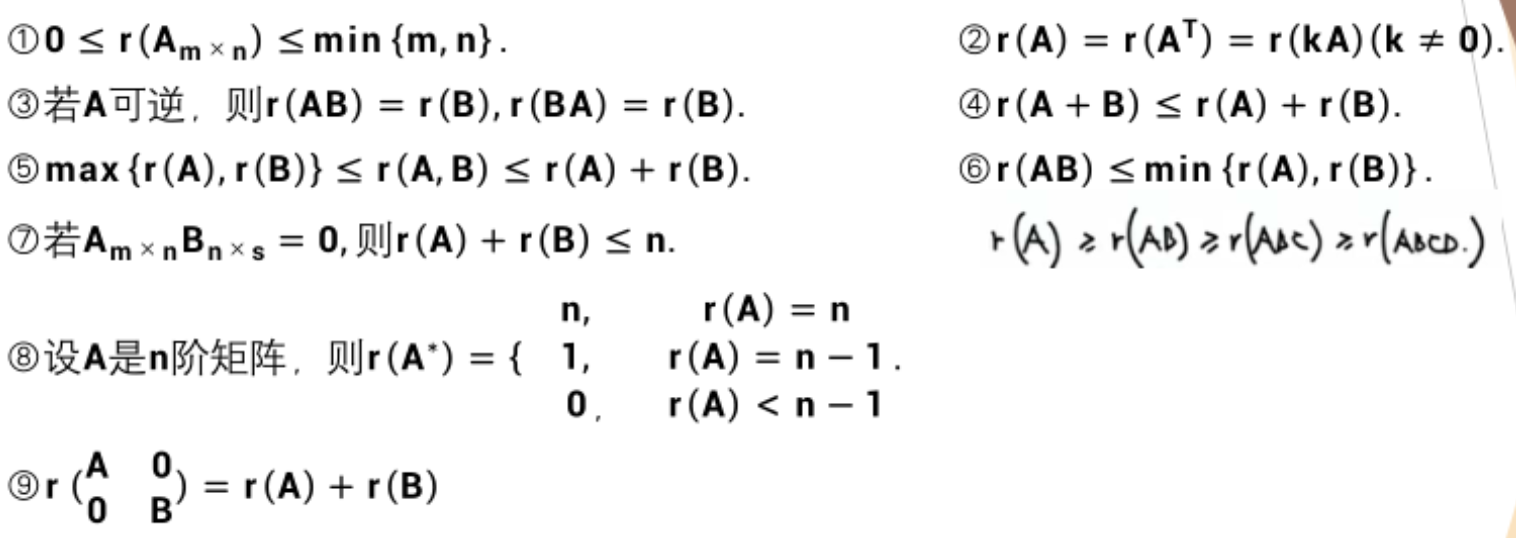
越乘越小，越拼越大（两个矩阵连起来），加起来最大

伴随矩阵

定义：对于n阶方阵 ，其伴随矩阵A^*是由A的代数余子式A_{ij}构成的n阶方阵，即

A^{*}=\begin{pmatrix}A_{11}&A_{21}&\cdots&A_{n1}\\A_{12}&A_{22}&\cdots&A_{n2}\\\vdots&\vdots&\ddots&\vdots\\A_{1n}&A_{2n}&\cdots&A_{nn}\end{pmatrix}其中A_{ij}是元素a_{ij}的代数余子式，A_{ij}=(-1)^{i + j}M_{ij}，这里在上面行列式章节的余子式小节有记载

对于二阶方阵，其伴随矩阵有个快速做法，即主对角线对换，副对角线变号

以下是一些关于伴随矩阵的性质：

AA^{*}=A^{*}A=\vert A\vert E \\ \vert A^{*}\vert=\vert A\vert^{n - 1}

关于伴随矩阵的秩：r(A^*)= \begin{cases} n\qquad r(A)=n \\ 1\qquad r(A)=n-1 \\ 0\qquad r(A)<n-1 \end{cases}

逆矩阵

定义：对于 n阶方阵A，如果存在n阶方阵B，使得AB=BA=E，则称 A是可逆的，且 B是 A的逆矩阵。若矩阵A是可逆矩阵，那么A的逆矩阵是唯一的，记为 A^{-1}=B

存在条件：矩阵A可逆\Leftrightarrow \vert A\vert \ne0

性质（前提是可逆）：

\vert A^{-1}\vert=\frac{1}{\vert A\vert} \qquad (A^{-1})^{-1}=A \\ (kA)^{-1}=\frac{1}{k}A^{-1} \qquad (AB)^{-1}=B^{-1}A^{-1} \\ (A^T)^{-1}=(A^{-1})^T（A,A^{T}均可逆的情况下）

二级结论： A^{-1}=\frac{1}{\vert A\vert}A^*

逆矩阵的求解：

  • 伴随矩阵法

求出伴随矩阵，再根据上面的二级结论即可算出逆矩阵

  • 初等变换法

将给出的矩阵A和单位矩阵E组成增广矩阵，通过初等变换将A变为单位矩阵，此时操作同步作用于单位矩阵E，直到A变为单位矩阵后，原单位矩阵E即是A的逆矩阵

向量

向量

向量没啥好说的，当成一维矩阵来看吧，向量组则可以当做矩阵。

线性组合和线性表示

非常简单的概念，放图不打了

2025.1.5博客更新日志 + ...
《幸福的勇气》观后感 + 2024...

Comment