Logo

Menu

江苏专转本-线性代数-Review

LiFasT
LiFasT
Published on 2025-01-07 / 43 Visits
0
0

前言

Preview是用来初次理解，而Review用来高效理解Preview并且面向题目的，可以把Review当做极速版

这里我会把要背的玩意放出来，集中背，然后丢一点典型题目复习

部分内容会关联到Preview里面，省的反复写了，Preview点此进入

黄色字体：表示定位

红色字体：强烈注意

绿色字体：做法指导

嘎嘎背就完了

逆序数、行列式的定义

首先必须知道行列式是行和列相等的，这个不知道可以直接进厂

先理清行列式的定义，即不同行不同列元素乘积的代数和，这部分内容在Preview-行列式-逆序数

逆序数是万物基础，需要完全理解，这部分也在Preview-行列式-逆序数

行列式五个性质

这部分内容在Preview-行列式-行列式的性质

五个性质比较重要，下面复述一下：

  • 性质一：经转置行列式的值不变

\begin{align*} \vert A^T\vert=\vert A\vert \end{align*}

  • 性质二：互换行列式的两行（列），行列式变号——即行列式前面加个负号

推论：如果行列式有两行（列）完全相同，则此行列式等于零

  • 性质三：若行列式某行（列）有公因子k，则可把公因子k提到行列式外面

注意：提公因子只能提一行（列）！！！

推论：行列式中如果有两行（列）元素成比例，则此行列式等于零

  • 性质四：行列式的某一行（列）的各元素乘以同一个数然后加到另一行（列）对应的元素上去, 行列式的值不变

  • 性质五：若行列式的某一行（列）的元素都是两数之和，则此行列式等于两个行列式之和

余子式和代数余子式

这俩玩意也是万物基础，请分清余子式和代数余子式

这部分内容在Preview-行列式-余子式和代数余子式

余子式：去掉所选元素的行和列的行列式

代数余子式：-1的（行+列）次方 * 余子式

其次，非常重要的一条：行列式某行（列）元素与另一行（列）元素代数余子式乘积之和等于0

为什么：因为如此操作就等于有两行or列相同元素了

范德蒙行列式、克拉默法则

这部分内容分别在Preview-行列式-范德蒙行列式和Preview-行列式-克拉默法则

比较简单就是套公式，背熟就行

行列式的计算

展开法

这部分内容在Preview-行列式-行列式计算方法-根据展开定理计算（分块法）

切记，展开要用对应元素乘代数余子式，不要忘了对应元素乘

化成上下三角

计算方法在Preview-行列式-行列式计算方法-根据性质转换（变为上下三角后定义算）

三角型行列式在Preview-行列式-行列式的种类-上三角、下三角行列式

暴力算法

这里补充一下，只有三阶和二阶能用暴力算，四阶就要考虑排列的问题了，所以四阶你还暴力算，要不人才要不傻卵

矩阵的乘法

矩阵是一个数表，请不要和行列式混起来

矩阵的乘法其实在Preview讲的很清楚了，内容在Preview-矩阵-矩阵的运算-矩阵的乘法

大白话说也就是前一个矩阵的行乘后一个矩阵的列

这里补充一点特别容易犯错的点：乘法分左乘和右乘，对于一个等式，必须采用相同的乘才能保持等式不变

X=Y \\ AX=AY \\ XA=YA \\ AX\ne YA

矩阵转化行列式（方阵）

这里重中之重，大部分题目都是求矩阵的行列式。在此之前，我想再次重复一遍，请记住，行列式是行列相等的！！！所以只有方阵可以求行列式！！！

这里我把几乎所有的方阵求行列式的公式都列出来了，包括但不限于逆矩阵和伴随矩阵，有些公式确实非常不好理解，所以把这些玩意背熟了就行，不背完准备进厂：

\left|kA\right| = k^n\left|A\right|：想理解请参考行列式的性质三，在Preview-行列式-行列式的性质

\vert A\cdot B\vert=\vert A\vert\cdot\vert B\vert：这个比较复杂就不理解了，按照这个你可以推出如下

\vert A^2\vert = \vert A\vert^2：如此你也应该知道N次方等于什么

\vert A^T \vert = \vert A \vert：理解比较复杂，背熟就行

\vert A^*\vert=\vert A\vert^{n - 1}：理解这个不如直接背来得轻松

\vert A^{-1}\vert=\frac{1}{\vert A\vert}：这个其实可以理解为A的负一次方的行列式等于A的行列式的负一次方

方阵还有一个幂的概念，其实比较好理解，这部分内容在Preview-矩阵-方阵

矩阵的初等变换

对于初等变换的内容在Preview讲的相当清楚了，你可以在Preview-矩阵-矩阵的初等变换看到

这里补充一些关于初等矩阵的内容：左乘一个初等矩阵就是对这个矩阵进行和此初等矩阵相同的行操作；右乘一个初等矩阵就是对这个矩阵进行和此初等矩阵相同的列操作

矩阵的类型

这部分内容也是相当清楚，在Preview-矩阵-矩阵的类型可以看到

这里把关于矩阵转置的一些公式整理出来：

(A^T)^T = A \qquad (kA)^T = kA^T \qquad (A + B)^T = A^T + B^T \qquad (AB)^T = B^T A^T

伴随矩阵、逆矩阵

这部分内容仍然相当清楚，在Preview-矩阵-伴随矩阵、逆矩阵可以看到

补充一点解惑内容：

  • 一个矩阵乘伴随矩阵or逆矩阵，顺序可以交换，结果仍然相同

  • 伴随矩阵就是用代数余子式替换原来元素，再转置一下

请记忆如下内容：

逆矩阵存在条件：矩阵A可逆\Leftrightarrow \vert A\vert \ne0

AA^{*}=A^{*}A=\vert A\vert E \\ \vert A^{*}\vert=\vert A\vert^{n - 1} \\ \vert A^{-1}\vert=\frac{1}{\vert A\vert} \qquad (A^{-1})^{-1}=A \\ (kA)^{-1}=\frac{1}{k}A^{-1} \qquad (AB)^{-1}=B^{-1}A^{-1} \\ (A^T)^{-1}=(A^{-1})^T（A,A^{T}均可逆的情况下） \\ A^{-1}=\frac{1}{\vert A\vert}A^*

矩阵的秩

这部分内容仍也相当清楚，在Preview-矩阵-矩阵的秩可以看到

子式的定义蛮难理解的，其实没那么多复杂的，如下：

对于方阵，直接算行列式，根据以下公式直接判断是否满秩

\vert A_n\vert \ne 0 \Leftrightarrow r(A_n) = n \\ \vert A_n\vert = 0 \Leftrightarrow r(A_n) < n

对于非方阵，咔咔一顿初等变换为阶梯型，算非零行个数

补充一点：满秩的方阵的N次方还是满秩

要背的内容其实挺多，背不下来就切记：越乘越小，越拼越大（两个矩阵连起来），（秩）加起来最大

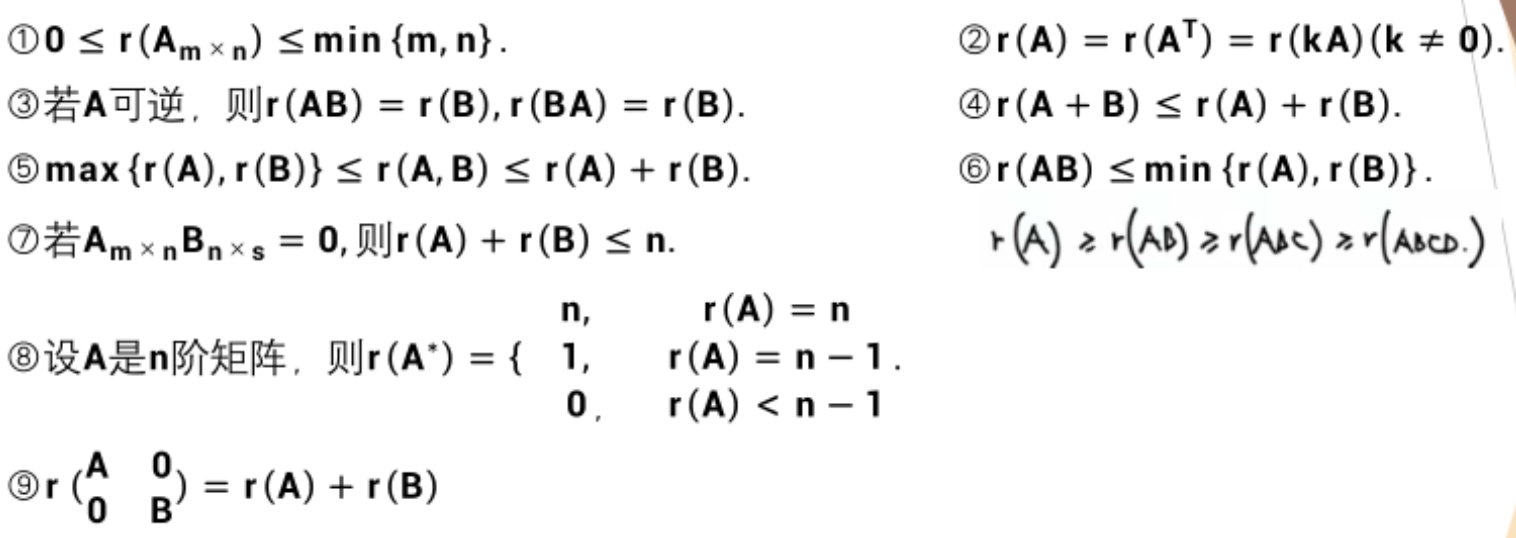
屏幕截图 2024-12-24 153326.png

线性相关的性质

  • 部分相关可以推出整体相关

  • 整体无关可以推出部分无关

  • n+1个n维向量必然线性相关（矩阵长方形就是线性相关）

极大线性无关组

极大线性无关组就是从一个大的向量组里面选出几个向量组成新的向量组，新的向量组可以线性标出原向量组的任意向量，且本身是线性无关

求解步骤：

  1. 向量组写成矩阵形式

  2. 进行初等变换为行阶梯型

  3. 非零行首个非零元所在列对应的向量就是极大线性无关组里的向量

方程组解的判定

齐次线性方程组至少有一个零解！！！

齐次线性方程组

系数矩阵是方阵的情况

直接算系数矩阵的行列式

\vert A_n\vert = 0 \Leftrightarrow Ax=0有无穷多解（非零解）\Rightarrow 线性相关 \\ \vert A_n\vert \ne 0 \Leftrightarrow Ax=0只有零解 （唯一解） \Rightarrow 线性无关

系数矩阵不是方阵的情况

算秩来判断

r(A)<n \Leftrightarrow Ax=0有无穷多解 （非零解）\Rightarrow 线性相关 \\ r(A)=n \Leftrightarrow Ax=0只有零解（唯一解） \Rightarrow 线性无关

非齐次线性方程组

通过对比系数矩阵的秩和增广矩阵的秩来判断

r(A)=r(A|B)<n \Leftrightarrow Ax=B有无穷多解 \Rightarrow 线性相关 \\ r(A)=r(A|B)=n \Leftrightarrow Ax=0只有唯一解 \Rightarrow 线性无关 \\ r(A)\ne r(A|B) \Leftrightarrow 无解

齐次线性方程组解的计算

  1. 方程组系数转为系数矩阵

  2. 系数矩阵进行初等变换为行最简形

  3. 找自由变量（非零行首个非零元之后的那一列对应的变量）

  4. 自由变量分别设为1回代计算其余的x

  5. 算出基础解系（基础解系就是刚才算的x组合）

  6. 通解=k_1基础解系_1+k_2基础解系_2

非齐次线性方程组解的计算

  1. 方程组系数转为系数矩阵

  2. 系数矩阵进行初等变换为行最简形

  3. 找自由变量（非零行首个非零元之后的那一列对应的变量）

  4. 自由变量设0求特解

  5. 自由变量分别设为1求基础解系

  6. 通解=特解+k_1基础解系_1

抓点典型

江苏专转本-极限-Review
2025.1.5博客更新日志 + ...

Comment