前言

不知道写啥，留个位置

嘎嘎背就完事了

两个重要极限

第二个重要极限有两种形式

等价无穷小

请记住只有x趋于0的时候才能等价无穷小替换

几个特殊的（不常见）：

无穷小的比较

如果\lim\frac{\alpha}{\beta}=0，就说\alpha是比\beta高阶的无穷小

如果\lim\frac{\alpha}{\beta}=\infty，就说\alpha是比\beta低阶的无穷小

如果\lim\frac{\alpha}{\beta}=c\neq0，则称\alpha与\beta是同阶无穷小

如果lim\frac{\alpha}{\beta}=1，则称\alpha与\beta是等价无穷小

连续性

判断函数在某点连续性方法如下：

• 该点函数值存在

• 该点极限值存在且等于函数值

算左极限和右极限，判断左极限是否等于右极限是否等于函数值

间断点

间断点分两类：第一类间断点、第二类间断点

第一类间断点

• 可去间断点

左右极限存在且相同，要么在此点函数没定义，要么在此点函数值与极限值不同

• 跳跃间断点

左右极限都存在但不相等

第二类间断点

• 无穷间断点

在某点单侧极限无穷大

• 震荡间断点

在接近该点时不断震荡

渐近线

这里只讨论水平渐近线和垂直渐近线

水平渐近线

设y=f(x)，若\lim_{x \to +\infty} f(x) = A_1或\lim_{x \to -\infty} f(x) = A_2，则y=A_1或y=A_2是曲线的水平渐近线

人话就是这个曲线趋于正无穷或者负无穷的值，y等于这个值就是水平渐近线

水平渐近线可能存在0到2条

垂直渐近线

设y=f(x)，若\lim_{x \to x_0^+} f(x) = \infty或\lim_{x \to x_0^-} f(x) = \infty，则x=x_0是曲线的垂直渐近线

人话就是这个曲线极限是无穷的这个点，x等于这个点就是垂直渐近线

垂直渐近线可能存在0到无数条

典型题目

无穷小的比较+变限积分+第一和第二个重要极限+洛必达

1. 无穷小比较，两个极限做除法

2. 变限积分，上限趋于下限，积分结果为0，因此洛必达

3. 变限积分求导，上限复合函数求导

4. 第一和第二个重要极限

5. 极限结果为常数，同阶不等价无穷小

洛必达

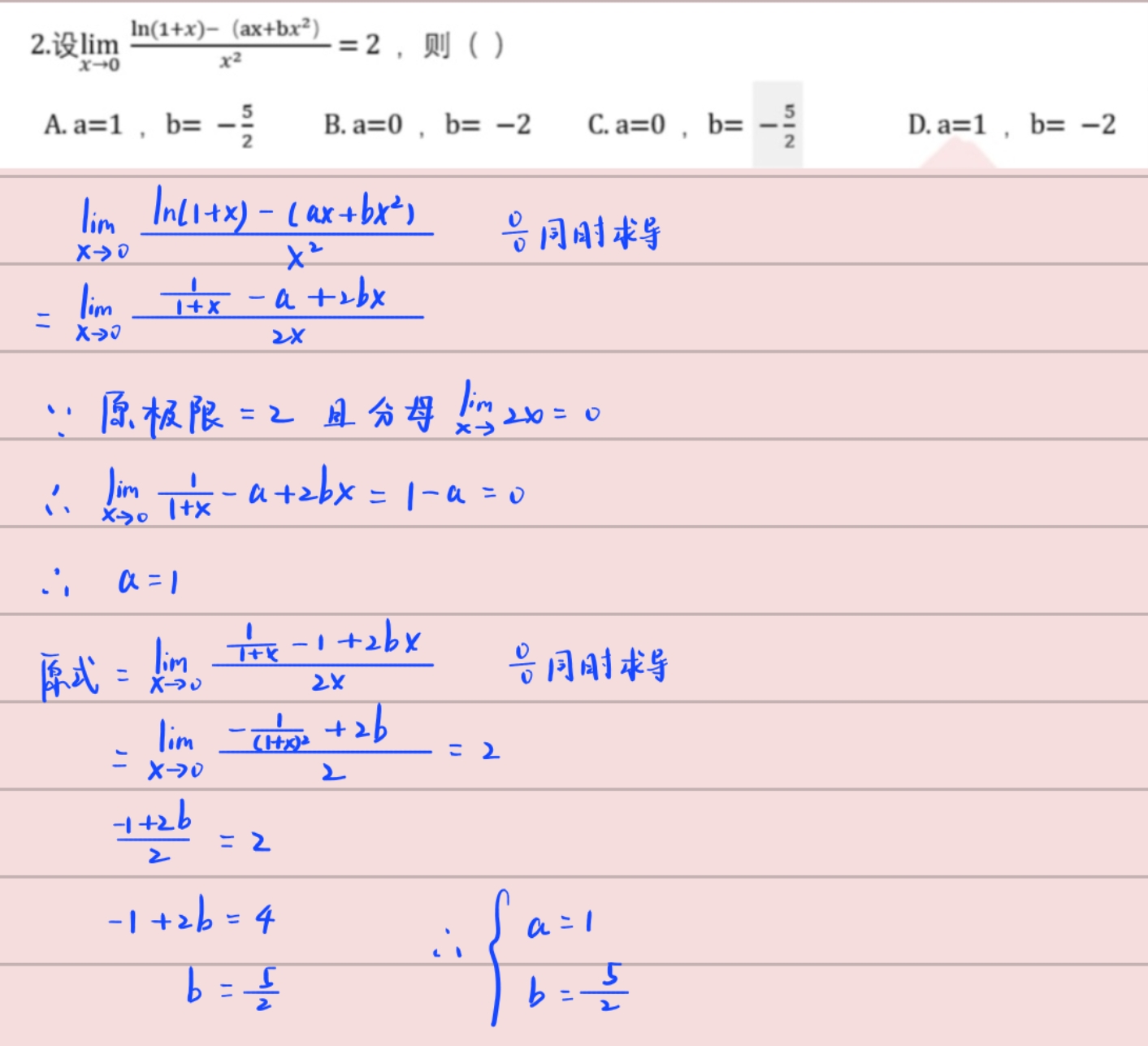
1. 洛必达，必须满足0比0或者无穷比无穷

对数恒等式+洛必达+0 \cdot \infty型转换为\frac{\infty}{\infty}型

1. 对于幂指函数，使用对数恒等式转换a^b=e^{\ln(a^b)}=e^{b\ln(a)}

2. 0 \cdot \infty型如图操作，变为\frac{\infty}{\infty}型进行洛必达

注：\lim_{x \to 0+} \ln(x) = -\infty

间断点+e^{\frac{1}{x}}

这题重点在于\frac{1}{x}的极限

即\begin{cases} \lim_{x \to x_0^+} \frac{1}{x} = +\infty \\ \lim_{x \to x_0^-} \frac{1}{x} = -\infty \end{cases}可得\begin{cases} \lim_{x \to x_0^+} e^\frac{1}{x} = +\infty \\ \lim_{x \to x_0^-} e^\frac{1}{x} = 0 \end{cases}

极限存在

这题重点在于C选项，上下虽然都是无穷但是不能使用洛必达，同时除以x解决

极限有理化

有理化之后分析即可，填空题过程不要求严谨

第二个重要极限

遇到1^\infin类型，转化为第二个重要极限\lim_{x \to 0}(1 + x)^{\frac{1}{x}} = e